Are you curious to know what is an oblique triangle? You have come to the right place as I am going to tell you everything about an oblique triangle in a very simple explanation. Without further discussion let’s begin to know what is an oblique triangle?
An oblique triangle is a type of triangle that does not have a right angle. In other words, all three angles in an oblique triangle are acute or obtuse. In this blog post, we will explore what an oblique triangle is, how to find its properties, and how to solve problems involving oblique triangles.
What Is An Oblique Triangle?
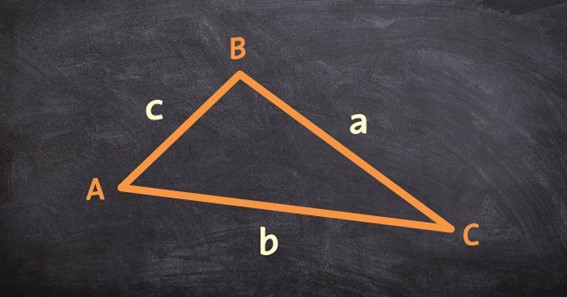
An oblique triangle is any triangle that does not have a right angle. Instead, all three angles are either acute (less than 90 degrees) or obtuse (greater than 90 degrees). The sides of an oblique triangle are also not equal in length, unlike an equilateral or isosceles triangle. Instead, each side length can be different.
Properties Of An Oblique Triangle
An oblique triangle has several properties that can be used to find its side lengths and angles. These properties include:
- The Law Of Cosines: This law can be used to find the length of any side of an oblique triangle, given the lengths of the other two sides and the angle between them. The formula is:
c² = a² + b² – 2ab cos(C)
where c is the length of the side opposite angle C, a and b are the lengths of the other two sides, and C is the angle between sides a and b.
- The Law Of Sines: This law can be used to find the length of any side of an oblique triangle, given the length of another side and the angle opposite it. The formula is:
sin(A) / a = sin(B) / b = sin(C) / c
where A, B, and C are the angles of the triangle, and a, b, and c are the lengths of the sides opposite those angles.
- The Pythagorean Theorem: This theorem can be used to find the length of the hypotenuse of a right triangle, but it can also be used to find the length of a side in an oblique triangle if one of the angles is 90 degrees. The formula is:
a² + b² = c²
where a and b are the lengths of the two legs of the right triangle, and c is the length of the hypotenuse.
Solving Problems Involving Oblique Triangles
To solve problems involving oblique triangles, it is important to first identify which properties can be used to find the missing side lengths or angles. For example, if you know the length of two sides and the angle between them, you can use the Law of Cosines to find the length of the third side. Or if you know the length of one side and the angles opposite it, you can use the Law of Sines to find the length of another side.
It is also important to keep in mind the properties of angles in a triangle. The sum of the three angles in a triangle is always 180 degrees, so if you know two angles, you can find the third by subtracting the sum of the other two from 180 degrees.
Conclusion
In conclusion, an oblique triangle is a triangle that does not have a right angle. It can have acute or obtuse angles, and its sides can be of different lengths. The properties of oblique triangles, such as the Law of Cosines, Law of Sines, and Pythagorean Theorem, can be used to find the missing side lengths and angles. By understanding the properties of oblique triangles, you can solve problems involving these types of triangles and gain a better understanding of geometry.
Learn more fun facts on Cricfor.
Click here – What Is Primer Dimer?
FAQ
What Best Describes An Oblique Triangle?
An oblique triangle is a triangle with no right angle. An oblique triangle has either three acute angles or one obtuse angle and two acute angles. In any case, as in any triangle, the sum of all three angles is equal to 180 degrees.
What Are The 2 Classifications Of Oblique Triangles?
An oblique triangle does not have a right angle and can also be classified as an acute triangle or an obtuse triangle.
What Are Oblique Triangle Examples?
Example: In the oblique triangle ABC side a = 6 cm, angles, a = 38° and g = 120°, find the remaining sides b and c and angle b. Solution: Given a = 6 cm, a = 38° and g = 120°. b, c, and b =? Example: In the oblique triangle with sides, b = 7 cm and c = 4 cm, and angle b = 115°, find side a and angles, a and g.
What Defines An Oblique Shape?
In math, this adjective refers to geometric lines or planes that are not parallel or perpendicular to a line or surface. A playground is positioned at an oblique angle to the ground.
Click here – What Is Droploads Driver?
I Have Covered All The Following Queries And Topics In The Above Article
What Is An Oblique Triangle
What Is An Oblique Line In A Triangle
What Is An Oblique Triangle?
Oblique Triangle Formula
Oblique Triangle Calculator
Oblique Triangle Law Of Sines
What Are The Four Cases Of Oblique Triangles And Their Solutions?
Oblique Triangle Trigonometry
Oblique Triangle Law Of Cosine
Oblique Triangle Given Only All The Angles.
What Is An Oblique Triangle
What is an oblique triangle?
What are three possible oblique triangle problem situations?